[컴퓨팅 사고] 논리 / 명제 / 증명

프로그래밍이 어려운 이유
- 언어 문법, 라이브러리

최초로 배울 떄 어려울 수 있으나 훈련에 비례하여 늘어남

- 논리 : Hard Logic (★)

 

 

 

논리

-  ex) 카드 문제

사실 : 모든 카드의 한쪽에는 알파벳이, 다른 쪽에는 숫자가 써있음
주장 : 만약 한쪽이 D 이면 반대쪽은 3
주장이 사실인지 확인하기 위해 다음 카드들 중 반드시 뒤집어 보아야 하는 것은 몇 개이고 어느 것인가?

답 : D와 7
핵심 : 영어면이 D인 경우에 무조건 숫자면이 3이 와야하는 것이지, 숫자면이 3이라고 무조건 D여야 할 필요는 없다.
-> 7뒤에 D가 있는 경우 주장이 성립하지 않으므로 7을 뒤집어야 한다.


- 직관적 논리(Soft Logic) vs 진짜 논리(Hard Logic) 
사람은 논리적으로 부정확한 Soft Logic을 사용하지만 컴퓨터는 Hard Logic을 사용함
-> 알고리즘을 Soft Logic으로 이해하고 풀려고 함


- 알고리즘을 봐도 이해가 안되는 이유 
1. 증명을 안봄 

2. 증명을 봐도 이해를 못하면 직관을 쓰려고 함 
-> 직관을 통해서 문제의 완전한 이해를 하는 것은 불가능

 

 

 

명제

- 연결사
~ : 부정
∧ : and
∨ : or
→ : 조건문 (~이라면)
↔ : 쌍조건문 (오직 P인 경우에만 Q이다)

 

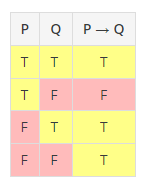
- 조건문
p이면 q이다 == p → q

전체 명제(p → q)가 거짓인 경우는, p가 참이고 q가 거짓인 경우만 해당한다! 
-> (T → F 인 경우에만 결과 F, 나머지는 결과가 모두 T) -> 참거거
 
p가 거짓이라면, 전체 명제(p → q)는 항상 참이다.
q가 참이라면, 전체 명제(p → q)는 항상 참이다.

조건문 결과

- 조건문의 역, 이, 대우

역 : 순서를 뒤집음 (p → q) -> (q → p)

이 : 명제 자체를 부정 (p → q) -> (~p → ~q)

대우 : 역과 이를 동시에 적용

조건문의 역, 이, 대우

 

- 쌍조건문

p이면 q이고, q이면 p이다 == p ↔ q

쌍조건문 결과

 

 

- 항진명제 : 모든 경우에 대해 항상 참인 명제

- 모순명제 : 모든 경우에 대해 항상 거짓인 명제

항진명제와 모순 명제는 성분명제의 값과 상관없이, 명제 자체가 가지는 구조에 따라서 결정됨

 

 

 

증명

정확한 명제식으로 표현할 수 있는 것

보통 정확한 명제식으로까지 쓰지는 않으나 근본적으로는 변환이 가능함

증명에서 조건문과 쌍조건문의 혼동으로 인해 문제가 발생함

 

 

수학적 귀납법 : P(1)이 참이고, P(n) → P(n+1)이 참이면 P(n)은 모든 자연수 n에 대해서 참이다.

 

코딩문제는 Hard Logic(ex. 수학적 귀납법)을 통해서 문제를 해결(증명)할 수 있어야 함

0. 문제를 증명이 가능한 명제로 바꿈 ( ex. sum(x)가 리턴하는 값은 1+2+...+x의 값과 항상 같다. )

 

1. P(1)이 참이다

-> 리턴 값으로 확인

 

2. P(x) → P(x+1)이 참이다

-> sum(x-1)이 1 + 2 + .. + (x - 1)을 리턴하면, sum(x)는 1 + 2 + .. + x를 리턴함을 증명하면 됨

 

 

 

 

- Reference

https://swexpertacademy.com/main/learn/course/subjectDetail.do?courseId=AVuPCwCKAAPw5UW6&subjectId=AV1lGbkqAAQCFAb_&& 

 

https://namu.wiki/w/%EB%AA%85%EC%A0%9C