[선형대수] 열 공간
벡터의 곱 표현 방법
1) 행열을 통한 표현
$Ax = \begin{vmatrix}
2x_{1} & 3x_{2} \\
2x_{1} & 4x_{2} \\
3x_{1} & 7x_{2} \\
\end{vmatrix}$
2) 벡터의 일차결합을 이용한 표현
$Ax = x_{1}\begin{vmatrix}
2 \\
2 \\
3 \\
\end{vmatrix} + x_{2}\begin{vmatrix}
3 \\
4 \\
7 \\
\end{vmatrix}$
이때 $a_{1}$과 $a_{2}$를 각각$\begin{vmatrix}
2 \\
2 \\
3 \\
\end{vmatrix}, \begin{vmatrix}
3 \\
4 \\
7 \\
\end{vmatrix}$에 대응 시킴
$x_{1}$과 $x_{2}$는 스칼라 곱이라고 할 수 있음
최종식은 $a_{1}$과 $a_{2}$의 일차 결합
벡터의 일차 결합
두 벡터 $v_{1}$, $v_{2}$의 일차 결합은 임의의 스칼라 $x_{1}$, $x_{2}$에 대해서,
$x_{1}v_{1}$, $x_{2}v_{2}$로 표현이 가능한 경우 벡터의 일차 결합이라고 한다.
열 공간
벡터의 집합
C(A)로 기호 표현
A의 열공간 : A의 열벡터 (a1, a2)의 일차결합으로 표현되는 모든 벡터의 집합
2개의 열을 가지고 2차원 평면을 만들 수 있음
ex) $x_{1}a_{1}$, $x_{2}a_{2}$ 가 있을 때,
경우 1) $x_{2}=0$ : $A_{x} = x_{1}a_{1}$ ($a_{1}$ 벡터만 표현)
경우 2) $x_{1}=0$ : $A_{x} = x_{2}a_{2}$ ($a_{2}$ 벡터만 표현)
경우 3) $x_{1},x_{2}=0$ : (0,0,0)
경우 4) $x_{1}\neq 0, x_{2}\neq 0$ : $a_{1}$과 $a_{2}$로 이루어진 2차원 평면 생성
-> 1차원과 1차원의 결합을 하면 2차원 평면이 만들어짐 ($x_{1}\neq 0, x_{2}\neq 0$)
C(A) (열공간)는 3차원 공간의 부분 공간 (평면이므로 3차원 공간은 아님)
선형방정식 계의 해가 존재하면 C(A)에 포함된다.
-> 명제(p -> q가 참이면, ~q -> ~p가 참이다)에 의해서,
$b\notin C(A) \Rightarrow A_{x}=b$의 해가 존재하지 않는다.
해의 존재 여부는 열벡터를 보면 알 수있다.
1) 연립 방정식을 이용한 해를 구하여 다른 식에 대입하여 확인
2) 역행렬을 통해 해를 찾아 해를 다른 식에 대입하여 확인
문제
예3) 각 열공간 물음?
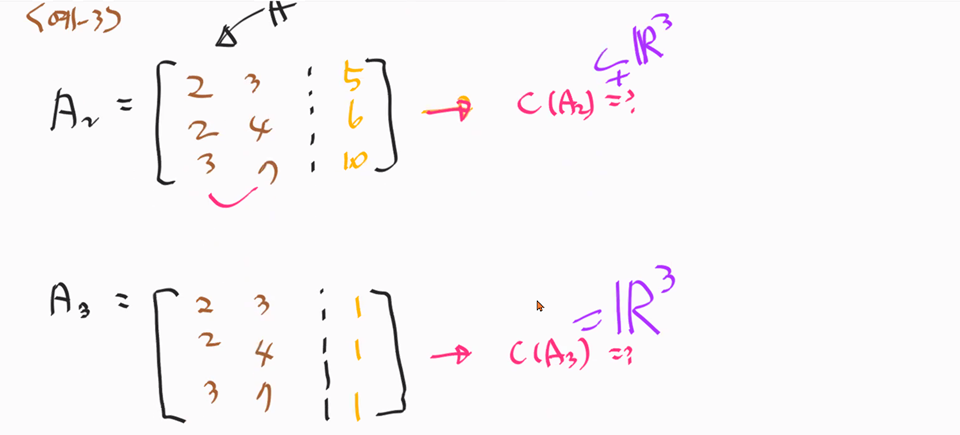
A2의 경우 2+3 -> 5, 2+4 -> 6, 3+7 -> 10이라는 규칙성에 의해서 $R^{3}$와 같지 않음 (도형이 아님)
조금 더 보충이 필요한듯
문 1)

(1번 풀이)

(2번 풀이)

?????????? 이번주의 주제 : 정방행렬이 아닌 행렬에서 해가 있는지 유무를 파악하는 방법
?????????? 열 공간의 사용 이유 : 해가 공간에 포함되는지 확인하기 위해서
'개인 공부 > 컴퓨팅 수학' 카테고리의 다른 글
| [선형대수] 기저, 독립 (1) | 2022.09.21 |
|---|---|
| [수치해석] 행렬식 (0) | 2022.09.18 |
| [기초통계학] 통계 (0) | 2022.04.08 |
| [기초통계학] 확률 (0) | 2022.04.07 |
| [기초통계학] 수열 (0) | 2022.04.06 |





