[수치해석] 크래머 공식 / 가우스 소거법
2022. 9. 22. 18:19
방정식의 해를 찾는 방법 : 크래머 공식, 가우스 소거법
크래머 공식
행렬식(det)를 사용하여 문제를 해결
성능 : $O(n!)$
$x_{i}=\frac{det(A(i))}{det(A)}, i=1, 2, .., n$
가우스 소거법
성능 : $O(n^{3})$ (크래머에 비하여 속도가 훨씬 빠르다)
해를 찾기 쉬운 행렬 : 항등 행렬, 삼각 행렬
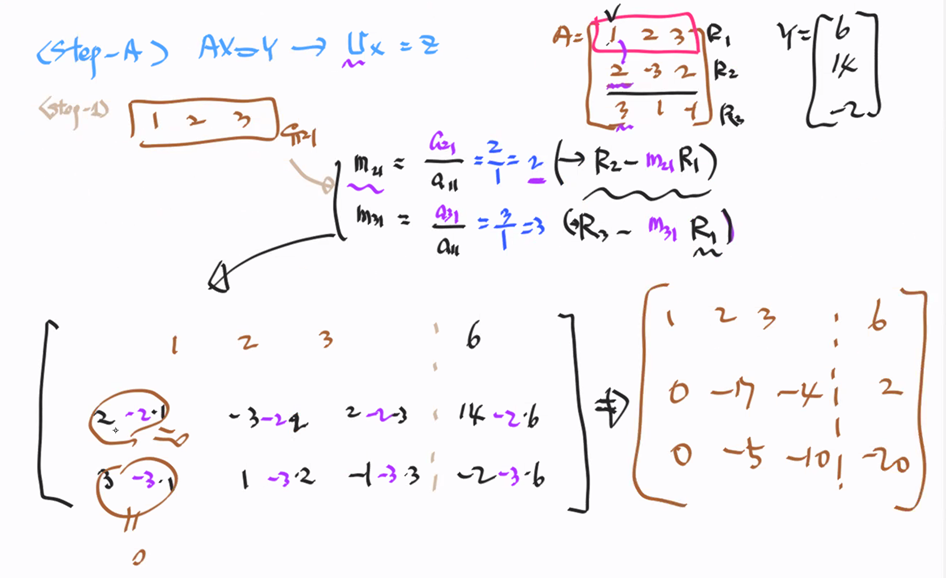
가우스 소거법은 소거를 통해 행렬을 변형하여 상삼각 행렬로 만듦
순서 : 확장행렬 -> 전방 소거 -> 후방 대입
위에서부터 차례대로 앞의 열을 소거해나감 -> 아래에서부터 하나씩 대입을 통해 해를 구해나감
확장 행렬 : 고정된 값x를 제외한 A와 Y를 모아서 만든 행렬
소거 시 $\frac{제거할-행의-요소}{유지할-행의-요소}$로 제거할 행을 모두 곱함

팁 : 숫자의 자릿수를 알고 싶은 경우 로그를 취하면 됨
'개인 공부 > 컴퓨팅 수학' 카테고리의 다른 글
| [컴퓨팅 사고] 논리 / 명제 / 증명 (0) | 2023.01.09 |
|---|---|
| [선형대수] 기저, 독립 (1) | 2022.09.21 |
| [수치해석] 행렬식 (0) | 2022.09.18 |
| [선형대수] 열 공간 (0) | 2022.09.17 |
| [기초통계학] 통계 (0) | 2022.04.08 |





