[기초통계학] 벡터와 공간
선형대수 유형
스칼라, 벡터, 행렬, 텐서
스칼라
숫자 하나로 이루어진 데이터
소문자 x로 표현
$x\in R$ (R은 실수 원소 집합을 의미)
벡터
방향과 순서를 가지고, 차원의 공간에 존재하는 점
데이터의 묶음
$x\in R^{n}$ (n은 벡터가 가지는 데이터의 개수)
행렬
2차원 배열
대문자 X로 표현
※ 한 사람에 대한 데이터를 표현할 때 벡터는 열로 되어 있으나, 행렬에서는 행으로 표현함
$x\in R^{n\times m}$ (행열을 R의 지수로 표기)
텐서
3차원 이상의 배열
이미지의 채널 등을 표현할 때 사용
벡터
- 기하학적
크기와 방향을 가진 물리량
시작점에서 끝점까지 연결한 화살표
- 대수적
파이썬 등에서 행 벡터, 열 벡터로 사용하는 경우 원소를 가지는 순서쌍으로 사용
벡터의 특징
1) 방향성을 가짐
2) 크기와 방향성을 가짐 (좌표의 어디에서 시작하는지는 중요하지 않음)
크기와 방향이 같으면 동일한 벡터
3) 같은 벡터라고 해서 좌표상의 위치가 동일한 것은 아님 (2번과 함께 생각하면 쉬움)
4) 크기가 같더라도 방향이 다르면 다른 벡터
백터의 표현
- 기하학적 표기
$\vec{AB}$ or $\vec{v}$
- 대수적 표기$x = (x_{1}, x_{..}, x_{n}) =
\begin{vmatrix}
x_{1} \\
x_{..} \\
x_{n} \\
\end{vmatrix}$
특수한 벡터
단위 벡터
길이가 1인 벡터, 방향 성분만 나타냄 (크기에는 영향을 미치지 않음)
벡터의 크기 = $\sqrt{x^{2} + y^{2}}$
$\vec{v}$에 대한 단위 벡터(u) = $\frac{\vec{v}}{\vec{v}의 크기}=\begin{bmatrix}
\frac{x}{\sqrt{x^{2}+y^{2}}} & \frac{y}{\sqrt{x^{2}+y^{2}}} \\
\end{bmatrix}$
위치 벡터
원점이 시작점에 있지 않은 벡터를 원점이 시작점인 벡터로 표현하는 방법
- 위치 벡터 성분 구하는 방법
1단계 : 원점 벡터를 시작점으로 하는 벡터를 표현 (원 점 벡터를 사용한 두 벡터를 그림)
2단계 : 벡터의 뺄셈 연산을 수행 (끝점에서 시작점 방향으로 진행 : 끝점 - 시작점)
ex) [(1,1) (3,4)]의 벡터
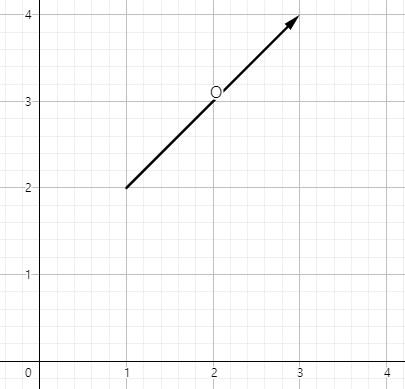
- 1단계 : 원점을 시작점으로 하는 A와 B를 생성
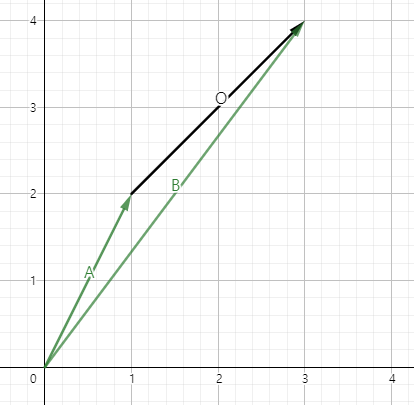
- 2단계 : B - A (끝점 - 시작점)
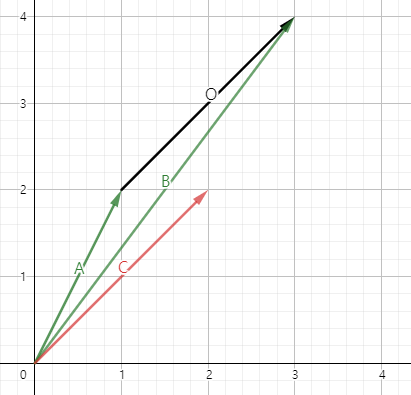
영 벡터
모든 성분이 0으로 구성된 벡터
크기가 0이면서, 시작점과 끝이 같은 벡터
- 영 벡터의 특징
0) 크기는 0이지만, 방향은 모든 방향
1) 어떤 벡터와도 평행
2) 어떤 벡터와도 같은 직선에 위치
3) 어떤 벡터와도 수직
4) 덧셈과 뺄셈의 항등원
선형 결합과 생성
선형 결합 : 벡터의 스칼라 곱과 덧셈을 조합하여 새로운 벡터를 얻는 연산
스칼라-벡터 곱 : 벡터의 길이를 늘리거나 줄임
두 벡터의 덧셈(뺄셈) : 두 벡터가 이루는 평행사변형의 대각선 값 (각 위치에 맞는 요소끼리의 합(차))
선형 독립과 선형 종속
선형 독립
$c_{1}a_{1} + .. + c_{n}a_{n}$ 수식을 만족하는 상수 값이 0이라면 선형 독립 ($c_{1} = c_{n} = 0$)
ex)
$\vec{v}=\begin{bmatrix}
1 \\3
\end{bmatrix},
\vec{w}=\begin{bmatrix}
2 \\-4
\end{bmatrix} $ 일 때,
각 벡터에 스칼라 곱을 곱하여 덧셈을 진행
$C_{1}\begin{bmatrix}
1 \\3
\end{bmatrix} +
C_{2}\begin{bmatrix}
2 \\-4
\end{bmatrix} $ $=\begin{bmatrix}
C_{1}+2C_{2} \\
3C_{1}-42C_{2}
\end{bmatrix}
=\begin{bmatrix}
0 \\
0
\end{bmatrix} $
위 결과로
$C_{1}+2C_{2}=0 $
$3C_{1}-42C_{2}=0 $
와 같은 식을 도출할 수 있으며, 이 방정식을 풀었을 때 $C_{1},C_{2}$가 0이라면 벡터는 선형독립임
선형 종속
$c_{1}, .. c_{n}$이 0이 아닌 값을 가질 때 종속
적어도 벡터 하나가 다른 벡터의 선형 결합으로 표현될 수 있어야 함 (다른 벡터의 연장)
또는 두 벡터의 선형 결합으로 다른 한 벡터를 표현 가능(두 벡터를 더한 값과 일치)한 경우 종속
벡터 공간과 부분 공간의 기저
벡터 공간
벡터가 모여 공간을 형성한 것
같은 공간상에 존재하는 벡터 사이에는 선형 결합 연산이 가능해야 함
같은 공간에서 선형 결합 연산이 가능한 벡터가 모인 집합
벡터 덧셈과 벡터-스칼라 곱의 연산에 닫혀 있는 벡터의 집합 (두 벡터를 더하거나, 스칼라곱이 가능한 공간)
벡터 공간의 표현
1) $x + y = (x_{1} + y_{1}, x_{2} + y_{2}, x_{3} + y_{3})$
2) $k\times x = (kx_{1}, kx_{2}, kx_{3})$
부분 공간
벡터 공간 $R^{n}$의 부분 공간으로 만든 공간을 전체 공간의 부분 공간($v$)이라고 함
- 부분 공간의 조건
1) $R^{n}$의 부분 공간 $v$는 영 벡터를 포함해야 함
2) 벡터 w가 벡터 공간 v에 포함되어 있다면, 벡터 w에 임의의 스칼라를 곱한 값 또한 v에 포함되어야 함
$\vec{w} \in v$고, c가 스칼라이면 $c\vec{w} \in v$이다.
3) 벡터 w와 벡터 u가 v에 포함되어 있다면, $\vec{w}+\vec{u}\in v$에 포함되어야 함
$\vec{w} \in v$고 $\vec{u} \in v$이면, $c\vec{w}+\vec{u} \in v$이다.
-> 뺄셈과 곱셈은 부분공간이 아님
부분공간의 기저
기저 : 벡터 공간을 생성하는데 최소한으로 필요한 것의 집합
- 기저의 특징
한 공간을 구성할 수 있는 벡터의 집합
차원에 따라 기저 벡터의 개수가 정해져 있음
2차원에서 기저 벡터의 개수는 2개
각이 0인 두 벡터는 하나만 있는 것과 동일하기 때문에 기저가 되지 않음
- 표준기저 벡터
여러 원소 중 하나만 값이 1이고, 다른 값은 0인 기저 벡터
ex. 3차원에 대한 표준 기저 벡터
$v_{1}=\begin{vmatrix}
1 \\
0 \\
0
\end{vmatrix},v_{2}=\begin{vmatrix}
0 \\
1 \\
0
\end{vmatrix},v_{3}=\begin{vmatrix}
0 \\
0 \\
1
\end{vmatrix}$
기저 벡터를 열로 가지는 행렬은 항등행렬이 됨
차원
수학에서 공간 내에 있는 점 등 위치를 나타내는데 필요한 축의 개수
선형대수학적 차원에서 차원은 기저 벡터의 개수를 의미함 (ex. 3차원 -> 3개의 기저 벡터, 10차원 -> 10개의 기저 벡터)
랭크
행렬에서 선형 독립인 행 혹은 열(벡터)의 개수
- 랭크의 성질
행렬 A의 랭크와 A의 전치 행렬이 같음
'개인 공부 > 컴퓨팅 수학' 카테고리의 다른 글
| [기초통계학] 벡터의 연산 (0) | 2022.03.20 |
|---|---|
| [기초통계학] 도함수의 활용 (1) | 2022.03.19 |
| [기초통계학] 다항함수의 미분 (0) | 2022.03.18 |
| [기초통계학] 미분 (0) | 2022.03.17 |
| [기초통계학] 지수 & 기하학 & 로그 (0) | 2022.03.16 |





