[기초통계학] 지수 & 기하학 & 로그
지수
지수 : 거듭제곱의 횟수를 나타내는 문자나 숫자
cf. y = an (a = 밑, n = 지수)
지수 법칙
합 : am * an = am+n
차 : am / an = am-n
곱 : (am)n = amn
거듭제곱 특징 (0이 아닌 경우에만 해당)
실수의 제곱은 항상 1임 : 20 = 1
실수의 1제곱은 실수 값과 동일함 : 21 = 2
실수의 음의 제곱은 ( 1 / 실수 제곱 ) : 2-1 = 1/2
거듭제곱근
제곱근 : 제곱의 반대가 되는 개념 (양수와 음수를 모두 포함함)
cf. 2는 8의 세제곱근, 8은 2의 세제곱
거듭제곱근의 성질
1) 거듭제곱근이 같은 곱셈과 나눗셈은 하나의 거듭제곱근으로 묶을 수 있음
2) 거듭제곱은 거듭제곱근 안으로 들어갈 수 있음
3) 거듭제곱근끼리 곱할 수 있음
4) 거듭제곱과 거듭제곱근은 약분이 가능함
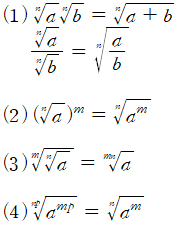
인수분해 공식
1) x2 + 2xy + y2 = (x + y)2
2) x2 - 2xy + y2 = (x - y)2
3) x2 - y2 = (x + y)(x - y)
4) x2 + (a + b)x + ab = (x + a)(x + b)
다항식의 곱셈
(a + b)(c + d) = ac + ad + bc + bd
기하학
삼각형 세 변의 길이와 각의 크기
(c = 빗변 : 직각 삼각형에서 대변, 3변 중에서 가장 긴 변)
- 예각 삼각형
C < 90도
c2 < a2 + b2
- 직각삼각형
C = 90도
c2 = a2 + b2 (피타고라스의 정리)
- 둔각삼각형
C > 90도
c2 > a2 + b2
지수함수
지수에 미지수 x가 있는 함수 (지수가 변수임)
밑은 양수여야 함, 0보다 크며 1이 아니어야 함
오차역전파 등에 사용
f(x) = ax (조건 : 0 < a < 1, a > 1)
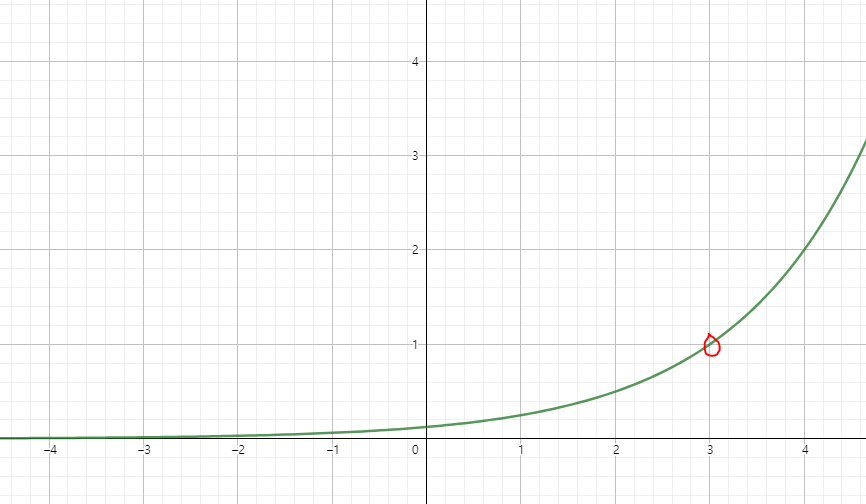
- a > 1일 때의 지수함수 그래프

- 0 < a < 1일 때의 지수함수 그래프

지수함수의 평행 이동
- x축 평행 이동
이동하고 싶은 만큼 지수에서 빼줌
f(x) = ax-p
cf. x축으로 3만큼 이동하고 싶은 경우 : f(x) = ax-3
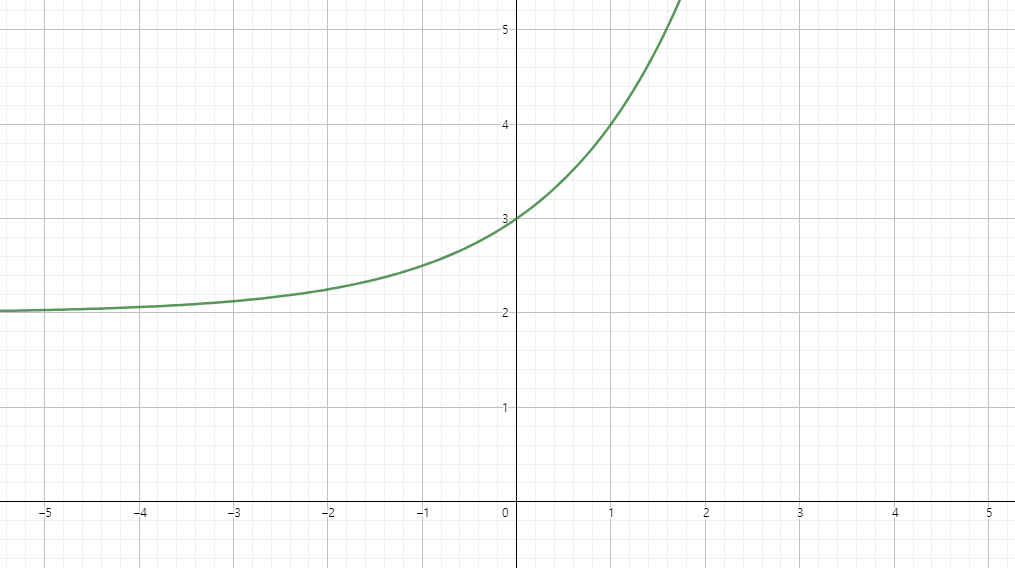
- y축 평행 이동
이동하고 싶은 만큼 상수를 더해줌
f(x) = ax + q
cf. y축으로 2만큼 이동하고 싶은 경우 : f(x) = ax + 2
f(0) = 1 + 2 = 3
지수함수의 대칭 이동
x축 대칭 이동
f(x) = a-x
y축 대칭 이동
f(x) = -ax
지수함수 이동 정리
x축 평행 이동 : f(x) = ax-p
y축 평행 이동 : f(x) = ax + q
x축 대칭 이동 : f(x) = a-x
y축 대칭 이동 : f(x) = -ax
로그함수
로그함수 : 로그의 진수나 밑에 미지수 x가 있는 함수
지수함수의 역함수
logax (a>0, a≠1, x>0) (a : 밑, x : 진수)
로그함수의 성질
logaxy = logax + logay
loga(1) = 0
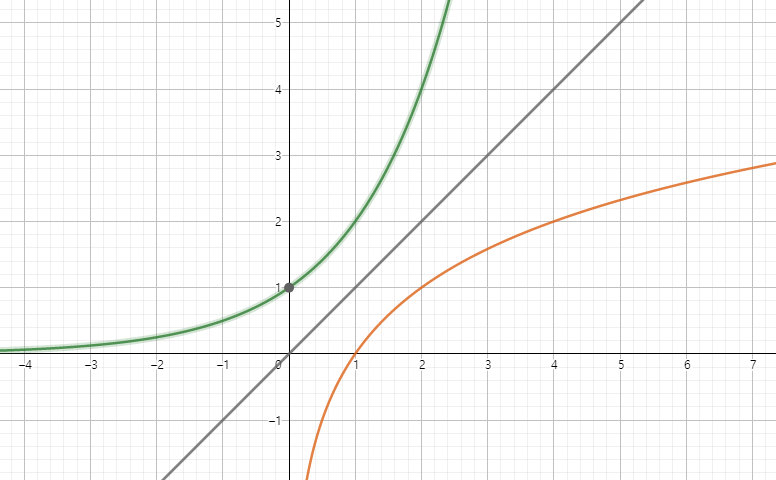
로그함수 그래프
로그함수는 지수함수의 역행렬이기 때문에 y = x에 대해 대칭적임
y = 2x
y = x
y = log2x
로그함수 이동
x축 평행 이동 : y = loga(x - p)
y축 평행 이동 : y = logax + q
x축 대칭 이동 : y = loga(-x)
y축 대칭 이동 : y = -logax
'개인 공부 > 컴퓨팅 수학' 카테고리의 다른 글
| [기초통계학] 도함수의 활용 (1) | 2022.03.19 |
|---|---|
| [기초통계학] 벡터와 공간 (0) | 2022.03.19 |
| [기초통계학] 다항함수의 미분 (0) | 2022.03.18 |
| [기초통계학] 미분 (0) | 2022.03.17 |
| [기초통계학] 기초 수학 (0) | 2022.03.15 |





