[알고리즘] 2차원 배열의 회전
2023. 1. 10. 16:19

다음과 같은 N*N 크기의 2차원 배열을 시계방향(오른쪽)으로 90도 회전한다면 아래 그림과 같습니다.

혹시 위 사진에서 규칙성을 찾으셨나요?
해당 배열을 인덱스로 본다면 좀 더 쉽게 규칙성을 찾을 수 있습니다.
행의 규칙성
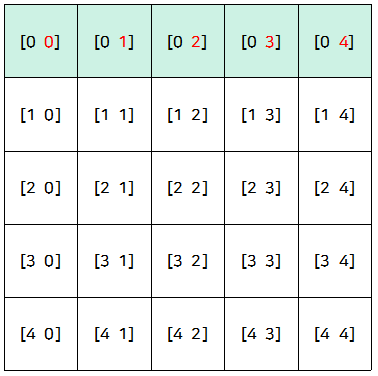

원본 배열과 회전 후 배열을 인덱스로 표현한다면 위와 같습니다.
잘 살펴보면 각각 기존의 열번호가 행번호로 적용되는 모습을 볼 수 있습니다.


행렬을 한 번 더 회전시킨다면 규칙성이 적용된다는 것을 더 쉽게 이해할 수 있는데요.
모든 요소들의 공통적인 열번호였던 4가 각각 행번호로 적용된 것을 확인할 수 있습니다.
-> 회전된 행의 인덱스 == 기존의 열 인덱스
열의 규칙성
열은 행보다는 조금(?) 어렵습니다.
회전한 행이 기존의 열을 사용하였듯이, 회전한 열도 기존의 행을 사용합니다.


위 이미지를 보시면 기존의 행과 회전된 열이 서로 다르다고 생각할 수 있습니다.
정확히는 회전한 열 인덱스 == N(행렬의 크기) - 기존의 행 인덱스 으로 변화 합니다.

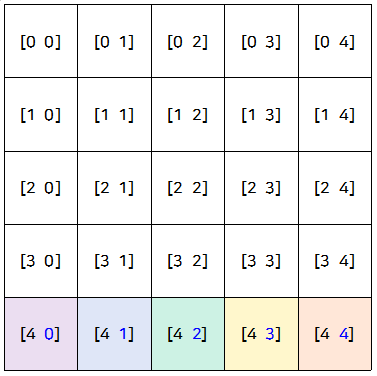
마찬가지로 한 번 더 살펴본다면 이해하기 쉬울텐데요.
전체 크기 N에서 기존 [0 4]의 행 번호인 0을 뺀 결과가 회전한 위치인 [4 4]의 열 번호가 된 것을 확인할 수 있습니다.
-> 회전된 열의 인덱스 == N - 기존의 행 인덱스
Python 예제 코드
N = 3
array = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]
temp = [[0] * N for _ in range(N)] # 결과를 저장하고 있을 변수
for i in range(N):
for j in range(N):
temp[j][N-i-1] = array[i][j] # 알고리즘 적용
print(temp) # [[7, 4, 1], [8, 5, 2], [9, 6, 3]]python을 통해 3*3 행렬의 회전을 구현한 예시 코드는 위와 같습니다.
'개인 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 최대공약수(GCD), 최소공배수 구하기 (유클리드 호제법) (0) | 2023.02.01 |
|---|---|
| [알고리즘] 소수 (Prime) (0) | 2023.01.27 |
| [코딩테스트] 최단 경로 알고리즘 (0) | 2022.11.23 |
| [코딩테스트] 다이나믹 프로그래밍 (0) | 2022.11.22 |
| [코딩테스트] 이진 탐색 알고리즘 (0) | 2022.11.21 |





